Kahend- ja kümnendsüsteem
Kui kümnendsüsteemis on arvude moodustamiseks kasutusel kümme numbrit 0…9, siis kahendsüsteemis on võimalik arve kirjutada vaid kahe numbri 0 ja 1 abil. Eksisteerib eeskiri, kuidas teisendada kümnendsüsteemi arve kahendsüsteemi ja vastupidi.
Teisendamine kahendsüsteemi
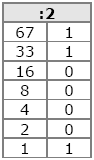 Kümnendarvu teisendamisel kahendarvuks tuleb seda jagada kahega senikaua kui see võimalik on. Kui jagamisel tekib jääk, on kahendarvu vastav järk 1, vastasel korral aga 0. Igal eelmise tehte tulemusena saadud jagatisest kasutatakse uuel jagamisel ainult arvu täisosa. Jagamise tulemusena saadud kahendarvu saab, kui lugeda seda märkivad nullid ja ühed altpoolt ülespoole. Seega arv 67 on kahendsüsteemis kirjutatuna 1000011.
Kümnendarvu teisendamisel kahendarvuks tuleb seda jagada kahega senikaua kui see võimalik on. Kui jagamisel tekib jääk, on kahendarvu vastav järk 1, vastasel korral aga 0. Igal eelmise tehte tulemusena saadud jagatisest kasutatakse uuel jagamisel ainult arvu täisosa. Jagamise tulemusena saadud kahendarvu saab, kui lugeda seda märkivad nullid ja ühed altpoolt ülespoole. Seega arv 67 on kahendsüsteemis kirjutatuna 1000011.
Teisendamine kümnendsüsteemi
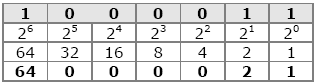 Kahendarvu teisendamisel kümnendsüsteemi tuleb kahendarvu alla kirjutada iga järgu kaalud. Kahendsüsteemi korral on nendeks kahe astmed. NB! Madalaima järgu kaal (mis asub kõige vasakpoolsemal positsioonil) on nullindal astmel! Seejärel korrutatakse kahendsüsteemi iga järk temale vastava kaaluga. On selge, et kui kahendarvus on vastava järgu koha peal väärtus null, on ka korrutis null. Kümnendarvu saamiseks tuleb saadud korrutised lihtsalt summeerida. Seega kahendarvu 1000011 väärtus kümnendsüsteemis on 1*64 + 0*32 + 0*16 + 0*8 + 0*4 + 1*2 + 1*1 = 67.
Kahendarvu teisendamisel kümnendsüsteemi tuleb kahendarvu alla kirjutada iga järgu kaalud. Kahendsüsteemi korral on nendeks kahe astmed. NB! Madalaima järgu kaal (mis asub kõige vasakpoolsemal positsioonil) on nullindal astmel! Seejärel korrutatakse kahendsüsteemi iga järk temale vastava kaaluga. On selge, et kui kahendarvus on vastava järgu koha peal väärtus null, on ka korrutis null. Kümnendarvu saamiseks tuleb saadud korrutised lihtsalt summeerida. Seega kahendarvu 1000011 väärtus kümnendsüsteemis on 1*64 + 0*32 + 0*16 + 0*8 + 0*4 + 1*2 + 1*1 = 67.
Ülesanne
- Koostada programm, mis teisendaks ette antud positiivse kümnendsüsteemi täisarvu kahendsüsteemi ja vastupidi.
- Programmi sisendiks võib olla nii kahend- kui kümnendsüsteemi arv.
- Programm peab väljastama nii sisestatud kui teisenduse tulemusena saadud arvu.
- Programm peab sisaldama elementaarset veakontrolli (kui sisestatud andmed ei ole numbrilisel kujul, kuisisestatud andmed puuduvad, kui sisestatud arv ei ole naturaalarv jne.)
- Teisendused arvusüsteemide vahel tuleb realiseerida algoritmiliselt, standardfunktsioone on lubatud kasutada vaid teisenduse õigsuse kontrolliks.